Answer: The equilibrium concentration of
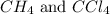 is 0.377 M and equilibrium concentration of
is 0.377 M and equilibrium concentration of
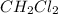 is 0.116 M
is 0.116 M
Step-by-step explanation:
To calculate the molarity of solution, we use the equation:
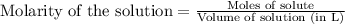
Volume of solution = 1 L
Moles of methane = 0.377 moles
Putting values in above equation, we get:
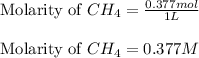
- For carbon tetrachloride:
Volume of solution = 1 L
Moles of carbon tetrachloride = 0.377 moles
Putting values in above equation, we get:

For the given chemical equation:
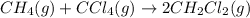
The expression for
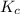 for the given equation follows:
for the given equation follows:
![K_c=([CH_2Cl_2]^2)/([CH_4][CCl_4])](https://img.qammunity.org/2020/formulas/chemistry/college/hvvxaqasset0xoqsets9qd1a9pa2rtpbt5.png)
We are given:
![K_c=9.52* 10^(-2)\\[CH_4]=0.377M\\[CCl_4]=0.377M]()
Putting values in above equation, we get:
![9.52* 10^(-2)=([CH_2Cl_2]^2)/((0.377)* (0.377))](https://img.qammunity.org/2020/formulas/chemistry/college/cdl6fk7lau9dyxcuzdhhcq0pxr4zzq109s.png)
![[CH_2Cl_2]=0.116M](https://img.qammunity.org/2020/formulas/chemistry/college/m2zwgophawfagbuukzz6gob4qjox9pqj3r.png)
Hence, the equilibrium concentration of
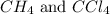 is 0.377 M and equilibrium concentration of
is 0.377 M and equilibrium concentration of
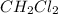 is 0.116 M
is 0.116 M