Question

Copper crystallizes with a face-centered cubic lattice and has a density of 8.93 g/cm3.

a.) Calculate the mass of one unit cell of copper (in grams) b.) Calculate the volume of the copper unit cell (in cm3). c.) Calculate the edge length of the unit cell (in cm). d.) Calculate the radius of a copper atom (in pm).

Answer 1

For a: The mass of one unit cell of copper is
`1.0553* 10^(-22)g`

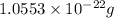
For b: The volume of copper unit cell is
`4.726* 10^(-23)cm^3`

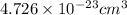
For c: The edge length of the unit cell is
`3.615* 10^(-8)cm`

For d: The radius of a copper atom 127.82 pm.

Step-by-step explanation:

• For a:

We know that:

Mass of copper atom = 63.55 g/mol

According to mole concept:

1 mole of an atom contains
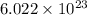`6.022* 10^(23)` number of atoms.

If,
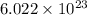`6.022* 10^(23)` number of atoms occupies 63.55 grams.

So, 1 atom will occupy =
`(63.55g)/(6.022* 10^(23)atom)* 1 atom=1.0553* 10^(-22)g`

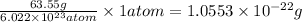
Hence, the mass of one unit cell of copper is
`1.0553* 10^(-22)g`

• For b:

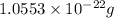
Copper crystallizes with a face-centered cubic lattice. This means that 4 number of copper atoms are present in 1 units cell.

Mass of 4 atoms of copper atom =
`1.0553* 10^(-22)g/atom * 4atoms=4.2212* 10^(-22)g`

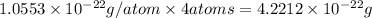
We are given:

Density of copper =
`8.93g/cm^3`

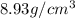
To find the volume of copper, we use the equation:

`\text{Density of copper}=\frac{\text{Mass of copper}}{\text{Volume of copper}}`

Putting values in above equation, we get:

`8.93g/cm^3=\frac{4.2212* 10^(-22)}{\text{Volume of copper}}\\\\\text{Volume of copper}=4.726* 10^(-23)cm^3`

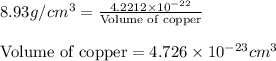
Hence, the volume of copper unit cell is
`4.726* 10^(-23)cm^3`

• For c:

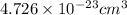
Edge length of the unit cell is taken as 'a'

Volume of cube =
`a^3`

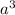
Putting the value of volume of unit in above equation, we get:

`\sqrt[3]{4.726* 10^(-23)}cm^3=3.615* 10^(-8)cm`

Hence, the edge length of the unit cell is
`3.615* 10^(-8)cm`

• For d:

The relation of radius and edge length for a face-centered lattice follows:

`a=r√(8)`

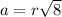
Putting values in above equation, we get:

`3.615* 10^(-8)=r√(8)\\\\r=1.2782* 10^(-8)cm`

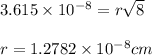
Converting cm to pm, we get:

`1cm=10^(10)pm`

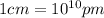
So,
`1.2782* 10^(-8)cm=127.82pm`

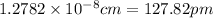
Hence, the radius of a copper atom 127.82 pm.