Answer : The work, heat during the process and the change of entropy of the gas are, 0 J, 3333.003 J and -10 J respectively.
Explanation :
(a) At constant volume condition the entropy change of the gas is:
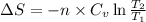
We know that,
The relation between the
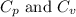 for an ideal gas are :
for an ideal gas are :

As we are given :
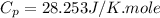

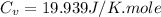
Now we have to calculate the entropy change of the gas.
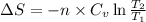
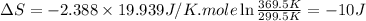
(b) As we know that, the work done for isochoric (constant volume) is equal to zero.
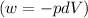
(C) Heat during the process will be,
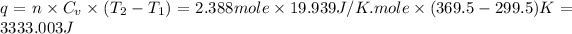
Therefore, the work, heat during the process and the change of entropy of the gas are, 0 J, 3333.003 J and -10 J respectively.