Question

A 0.0811 kg ice cube at 0 °C is dropped into a Styrofoam cup holding 0.397 kg of water at 14.8 °C. Calculate the final temperature of the system. Assume the cup and the surroundings can be ignored.

Answer 1

The final temperature of the system is 16.4°C.

Step-by-step explanation:

Given that,

Mass of ice cube = 0.0811 kg=81.1 g

Mass of water = 0.397 kg = 397 g

Initial temperature of ice cube = 0°C=273 K

Initial temperature of water = 14.8°C = 14.8+273=287.8 K

We need to calculate the final temperature

We know that,

Specific capacity of solid = 2.09 J/g°C

Using formula of energy

`E_(s)=E_(l)`

`mc_{p_(s)}(T_(f)-T_(i))=mc_{p_(s)}(T_(f)-T_(i))`

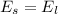
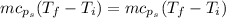
Put the value into the formula

`81.1*2.09(T_(f)-0)=397*4.18*(T_(f)-14.8)`

`169.5(T_(f)-0)=1659.5(T_(f)-14.8)`

`169.5T_(f)=1659.5T_(f)-24560.6`

`1490T_(f)=24560.6`

`T_(f)=(24560.6)/(1490)`

`T_(f)=16.4^(\circ)\ C`

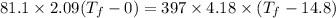
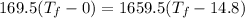
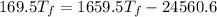
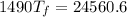
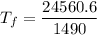
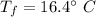
Hence, The final temperature of the system is 16.4°C.