Question

1) Let A = {1, 2, 3, 4} and R be a relation on the set A defined by: R = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (4, 1), (4, 4)} Determine whether R is reflexive, irreflexive, symmetric, asymmetric, antisymmetric, or transitive. For each property, either explain why R has that property or give an example showing why it does not. (30 points)

Answer 1

R is not reflexive,not irreflexive ,symmetric,not asymmetric,not antisymmetric and transitive.

Explanation:

1.Reflexive : Relation R is not reflexive because it does not contain identity relation on A.

Identity relation on A:{(1,1),(2,2),(3,3),(4,4)}

If we take a relation R on A :{(1,1),(2,2),(3,3),(4,4),(1,2),(2,1)}

The relation R is reflexive on set A because it contain identity relation.

2.Irreflexive: Given relation R is not reflexive because it contain some elements of identity relation .If a relation is irreflexive then it does not contain any element of identity relation. We can say the intersection of R with identity relation is empty.

`R\cap I=\left\{(1,1),(2,2),(4,4)\right\} \\eq \phi`

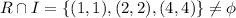
If we take a relation on A R:{(1,2),(2,1)}

Then relation is irreflexive because it does not contain any element of identity relation

`R\cap I=\phi`

3.Symmetric : The given relation R is symmetric because it satisfied the property of symmetric relation.

(1,2)belongs to relation (2,1) also belongs to relation ,(1,4) belongs to relation and (4,1) also belongs to given relation Hence we can say it is symmetric relation.

4.Asymmetric: The given relation is not asymmetric relation.Because it does not satisfied the property of asymmetric relation

Asymmetric relation: If (a,b) belongs to relation then (b,a) does not belongs to given relation.

Here (1,2) belongs to given relation and (2,1) also belongs to given relation Therefore, it is not asymmetric.

If we take a relation R on A

R:{(1,2),(1,3)}

It is asymmetric relation because it does not contain (2,1) and (3,1).

5.Antisymmetric: The given relation is not antisymmetric because it does not satisfied the property of antisymmetric relation.

Antisymmetric relation: If (a,b) and (b,a) belongs to relation then a=b

If we take a relation R

R;{(1,2) (1,1)}

It is antisymmetric because it contain (1,1) where 1=1 .Hence , it is antisymmetric.

6.Transitive: The given relation is transitive because it satisfied the property of transitive relation

Transitive relation: If (a,b) and (b,c) both belongs to relation R then (a,c) belongs to R.

Here, we have (1,2) and (2,1)belongs to relation then (1,1) and (2,2) are also belongs to relation.

(1,4) and (4,1) then (1,1) and (4,4) are also belongs to the relation.