Just fun I'm going to add something above the below.
You can write an equation for this without the parameter.
You have y=t+5 and x=2t. If you multiply both sides of y=t+5 by 2 you should get 2y=2t+10 and guess what you can replace 2t with x since you have x=2t. So you can write 2y=x+10 as your equation to represent the parametric version they have here.
This is a linear equation as our graph appears to be below. Solve for y by dividing both sides by 2 gives you y=x/2 +5. The slope is 1/2 and the y-intercept is 5. If t is between -2 and 3 then x is between -4 and 6 since x is doubled t (inclusive here since we have those equal signs along with those inequalities).
So you could have just graph the line y=x/2+5 on the interval
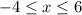 /
/
Anyways, I'm also going to look at this without the rewrite:
I'm going to make a table with 4 columns. The first column is t. The second is x(t), the third is y(t), and the fourth will be a list of points (x,y) our relation will go through).
t | x(t) | y(t) | (x,y)
------------------------------------------------------
-2 2(-2)=-4 -2+5=3 (-4,3)
-1 2(-1)=-2 -1+5=4 (-2,4)
0 2(0)=0 0+5=5 (0,5)
1 2(1)=2 1+5=6 (2,6)
2 2(2)=4 2+5=7 (4,7)
3 2(3)=6 3+5=8 (6,8)
Now I'm going to graph the points in the last column on a coordinate-plane.
The horizontal axis is your x-axis and the vertical axis is your y-axis. I did the x-axis going up or down by two's while the y-axis is going up and down only by one's.