Answer:
The null hypotheses that the magazine will test is
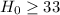 .
.
Alternative:
 .
.
Explanation:
The null hypotheses is the one which contains the equal sign, while the alternative hypotheses is the opposite of the null hypotheses.
In this problem, we have that:
The manufacturer of a certain engine treatment claims that if you add their product to your engine, it will be protected from excessive wear. An infomercial claims that a woman drove 33 hours without oil, thanks to the engine treatment.
This means that at the very least, due to treatment, the engine should have lasted 33 hours. So the null hypotheses that the magazine will test is
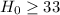 .
.
Otherwise, the engine may have lasted less than 33 hours. So
 .
.