Answer:
***********o o**************
<----------(-4)--------(-2)--------(0)--------(-2)----------(4)-------------->
x>4 or x<-4
Explanation:
You are looking for numbers that give you a distance, x, greater than 4 from 0. That wouldn't be anything between -4 and 4 because these would all give you a distance less than 4 from 0. So the answer would be to shade everything greater than 4 while also shading everything less than -4.
Here is a number line <-----|-----|-----|-----|-----|-----|-----|-----|-->
-6 -4 -2 0 2 4 6 8
Let's think about this more which of these numbers on this number line would satisfy |x|>4?
Numbers inside the numbers -4 and 4.
Or the numbers on the outside.
Let's try the inside numbers:
-2,02
|-2|>4
2>4 is false which means -2 doesn't satisfy |x|>4
|0|>4
0>4 is false which means 0 doesn't satisfy |x|>4
|2|>4
2>4 is false which means 2 doesn't satisfy |x|>4
We could also try -4 and 4... but these will both give you a distance equal to 4 from 0. And we are looking for greater than.
|-4|>4
4>4 is false which mean -4 doesn't satisfy |x|>4
|4|>4
4>4 is false which means 4 doesn't satisfy |x|>4
Now let's try the numbers on the outside:
-6,6,8
|-6|>4
6>4 is true so -6 does satisfy |x|>4
|6|>4
6>4 is true so 6 does satisfy |x|>4
|8|>4
8>4 is true so 8 does satisfy |x|>4
So what I'm trying to do is convince you more that the only numbers that would satisfy |x|>4 are numbers outside the interval from -4 to 4.
So x>4 or x<-4.
On a number line the solution would look like this:
***********o o**************
<----------(-4)--------(-2)--------(0)--------(-2)----------(4)-------------->
We have holes at -4 and 4 to mean we do not include those numbers. We would have if the inequality read
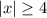 . The line underneath this inequality means to include or equals. We do not want to include; we did not have the equal sign. The only difference between the two solutions would be to fill the holes if you
. The line underneath this inequality means to include or equals. We do not want to include; we did not have the equal sign. The only difference between the two solutions would be to fill the holes if you
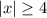 .
.