Question

Jayne is studying urban planning and finds that her town is decreasing in population by 3%

each year. The population of her town is changing by a constant rate.

True

False

Answer 1

True

Explanation:

Let,
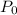`P_0` be the initial population,

Given,

The population is decreasing by 3% each year,

Thus, the population after t years would be,

`P=P_0 (1-(3)/(100))^t`

`\implies P=P_0(1+(-3)/(100))^t`

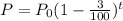
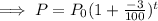
Since, if a population is changing by a constant rate then the population after t years is,

`P=P_0(1+(r)/(100))^t`

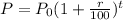
Where, r is the rate of changing per period.

Hence, in the given situation the population is changing by the constant rate.