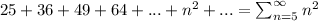Answer:
The sum using summation notation, assuming the suggested pattern continues is :
Explanation:
We are given a series of numbers as
25 + 36 + 49 + 64 + ... + n^2 + ...
To write the sum using summation notation means we need to express this series in terms of a general n such that there is a whole summation expressing this series.
Here we see that each of the numbers could be expressed as follows:
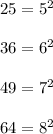
and so on.
i.e. the series starts by taking the square of 5 then of 6 then 7 and so on.
and the series goes to infinity.
Hence, the summation notation will be given by: