Answer: 0.0136
Explanation:
Given : Mean :
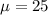
Standard deviation :
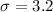
Sample size :

The formula to calculate the z-score :-
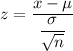
For x = 24
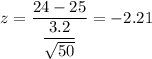
The p-value =
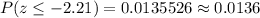
Hence, the probability that the sample mean age for 50 randomly selected women to marry is at most 24 years = 0.0136