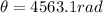Answer:
Part A)
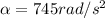
Part B)
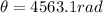
Step-by-step explanation:
Drill starts from rest so its initial angular speed will be
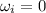
now after 3.50 s the final angular speed is given as
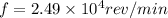
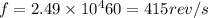
so final angular speed is given as
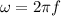
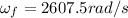
now we have angular acceleration given as
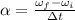

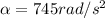
Part b)
The angle through which it is rotated is given by the formula
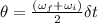
now we have