Question

Carbonyl fluoride, COF2, is an important intermediate used in the production of fluorine-containing compounds. For instance, it is used to make the refrigerant carbon tetrafluoride, CF4 via the reaction 2COF2(g)⇌CO2(g)+CF4(g), Kc=4.20 If only COF2 is present initially at a concentration of 2.00 M, what concentration of COF2 remains at equilibrium?

Answer 1

Answer: The concentration of
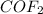`COF_2` remains at equilibrium is 0.40 M.

Explanation:-

Initial concentration of
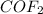`COF_2` = 2 M

The given balanced equilibrium reaction is,

`2COF_2(g)\rightleftharpoons CO_2(g)+CF_4(g`

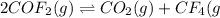
Initial conc. 2 M 0 0

At eqm. conc. (2-2x) M x M x M

The expression for equilibrium constant for this reaction will be,

`K_c=([CO_2]* [CF_4])/([COF_2]^2)`

Now put all the given values in this expression, we get :

`4.20=((x)* (x))/((2-2x)^2)`

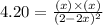
By solving the term 'x', we get :

x = 0.80 M

Thus, the concentrations of
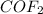`COF_2` at equilibrium is : (2-2x) = 2-2(0.80)=0.40 M

The concentration of
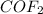`COF_2` remains at equilibrium is 0.40 M.