Answer:
a) The 99% confidence interval for the mean noise level = [122.44, 151.96]
b) Sample standard deviation, s = 17.3dB
Step-by-step explanation:
Noise levels at 5 airports = 147,123,119,161,136
Mean noise level
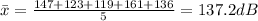
Variance of noise level
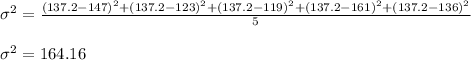
Standard deviation,
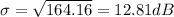
a) Confidence interval is given by
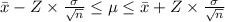
For 99% confidence interval Z = 2.576,
Number of noises, n = 5
Substituting
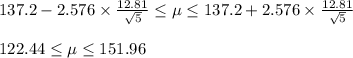
The 99% confidence interval for the mean noise level = [122.44, 151.96]
b) Sample standard deviation
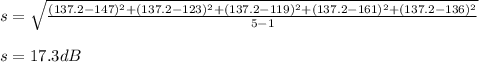
Sample standard deviation, s = 17.3dB