Question

Which shows x^2 + 2x = 3 as a perfect square equation? What are the solution(s)?

a. x^2+2x-3=0; -3 and 1
b. x^2+2x+1=0; -1
c. (x+1)^2=4; -3 and 1
d. (x+1)^2=0; -1

Answer 1

First we can rewrite the equation to,

`x^2+2x-3=0`

Which factors to,

`(x+3)(x-1)=0`

And this leads towards two solutions,

`x_1\Longleftrightarrow x+3=0\Longrightarrow x_1=-3`

and,

`x_2\Longleftrightarrow x-1=0\Longrightarrow x_2=1`

The answer is A.

Hope this helps.

r3t40

Answer 2

c

Explanation:

Given

x² + 2x = 3

To complete the square

add ( half the coefficient of the x- term )² to both sides

x² + 2(1)x + 1 = 3 + 1

(x + 1)² = 4 ( take the square root of both sides )

x + 1 = ±
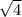`√(4)` = ± 2 ( subtract 1 from both sides )

x = - 1 ± 2, hence

x = - 1 - 2 = - 3 and x = - 1 + 2 = 1