Question

Which of the following values would you expect for the ratio of half-lives for a reaction with starting concentrations of 0.05M and 0.01M, t1/2(0.05M) / t1/2 (0.01M), if a reaction is known to be zero order?

Answer 1

The expected ratio of half-lives for a reaction will be 5:1.

Step-by-step explanation:

Integrated rate law for zero order kinetics is given as:

`k=(1)/(t)([A_o]-[A])`

`[A_o]` = initial concentration

[A]=concentration at time t

k = rate constant

if,
`[A]=(1)/(2)[A_o]`

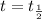`t=t_{(1)/(2)}`, the equation (1) becomes:

`t_{(1)/(2)}=([A_o])/(2k)`

Half life when concentration was 0.05 M=
`t_{(1)/(2)}`

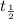
Half life when concentration was 0.01 M=
`t_{(1)/(2)}'`

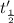
Ratio of half-lives will be:

`\frac{t_{(1)/(2)}}{t_{(1)/(2)}'}=(([0.05 M])/(2k))/(([0.01 M])/(2k))=(5)/(1)`

The expected ratio of half-lives for a reaction will be 5:1.