Question

An aircraft with a mass of 10,000 kg starts from rest at sea level and takes off, then flies to a cruising speed of 620 km/h and altitude of 10 km. Assume g = 9.8 m/s' throughout the process What is the aircraft's change in potential energy? What is the aircraft's change in kinetic energy? a. b. Answers: About 1000 and 150 MJ, respectively

Answer 1

The change in potential energy and kinetic energy are 980 MJ and 148.3 MJ.

Step-by-step explanation:

Given that,

Mass of aircraft = 10000 kg

Speed = 620 km/h = 172.22 m/s

Altitude = 10 km = 1000 m

We calculate the change in potential energy

`\Delta P.E=mg(h_(2)-h_(1))`

`\Delta P.E=10000*9.8*(10000-0)`

`\Delta P.E=10000*9.8*10000`

`\Delta P.E=980000000\ J`

`\Delta P.E=980\ MJ`

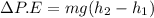
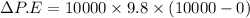
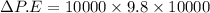
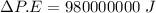
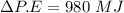
For g = 10 m/s²,

The change in potential energy will be 1000 MJ.

We calculate the change in kinetic energy

`\Delta K.E=(1)/(2)m(v_(2)^2-v_(1)^2)`

`\Delta K.E=(1)/(2)*10000*(172.22^2-0^2)`

`\Delta K.E=(1)/(2)*10000*(172.22^2)`

`\Delta K.E=148298642\ J`

`\Delta K.E=148.3\ MJ`

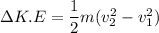
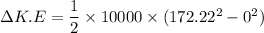
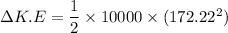
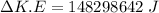
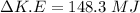
For g = 10 m/s²,

The change in kinetic energy will be 150 MJ.

Hence, The change in potential energy and kinetic energy are 980 MJ and 148.3 MJ.