Question

A parallel-plate air capacitor with a capacitance of 260 pF has a charge of magnitude 0.155 μC on each plate. The plates have a separation of 0.313 mm. What is the potential difference between the plates?

Answer 1

The potential difference between the plates is 596.2 volts.

Step-by-step explanation:

Given that,

Capacitance
`C=260\ pF`

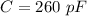
Charge
`q=0.155\ \mu\ C`

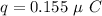
Separation of plates = 0.313 mm

We need to calculate the potential difference between the plates

Using formula of potential difference

`V= (Q)/(C)`

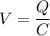
Where, Q = charge

C = capacitance

Put the value into the formula

`V=(0.155*10^(-6))/(260*10^(-12))`

`V=596.2\ volts`

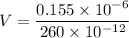
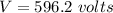
Hence,The potential difference between the plates is 596.2 volts.