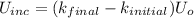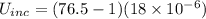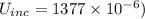Question

A1.0µF capacitor has a potential difference of 6.0 V applied across its plates. If the potential difference acro its plates is increased to 8.0 V, how much additional energy does the capacitor store? If the dielectric constant is changed from 1 to 76.5 how does this change the amount of charge stored on the capacitor plates?

Answer 1

14 x 10⁻⁶ J

1377 x 10⁻⁶ J

Step-by-step explanation:

C = Capacitance of the capacitor = 1 x 10⁻⁶ F

ΔV = Original potential difference across the plates = 6.0 Volts

U₀ = Original energy stored in the capacitor

Original energy stored in the capacitor is given as

U₀ = (0.5) C ΔV² eq-1

ΔV' = Potential difference across the plates after increase = 8.0 Volts

U'₀ = New energy stored in the capacitor

New energy stored in the capacitor is given as

U'₀ = (0.5) C ΔV'² eq-2

U = Additional energy stored

Additional energy stored by the capacitor is given as

U = U'₀ - U₀

U = (0.5) C ΔV'² - (0.5) C ΔV²

U = (0.5) (1 x 10⁻⁶) (8)² - (0.5) (1 x 10⁻⁶) (6)²

U = 14 x 10⁻⁶ J

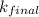`k_(final)` = final dielectric constant = 76.5

`k_(initial)` = initial dielectric constant = 1

Energy stored in the capacitor is directly proportional to the dielectric constant, hence increase in the energy is given as

`U_(inc)=(k_(final) - k_(initial))U_(o)`

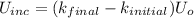
Original energy stored in the capacitor is given as

U₀ = (0.5) C ΔV² = (0.5) (1 x 10⁻⁶) (6)² = 18 x 10⁻⁶ J

`U_(inc)=(k_(final) - k_(initial))U_(o)`

`U_(inc) = (76.5 - 1)(18* 10^(-6))`

`U_(inc) = 1377* 10^(-6))`