Question

At takeoff, a commercial jet has a speed of 72 m/s. Its tires have a diameter of 0.89 m. Part (a) At how many rev/min are the tires rotating? Part (b) What is the centripetal acceleration at the edge of the tire in m/s^2?

Answer 1

a) Revolutions per minute = 2.33

b) Centripetal acceleration = 11649.44 m/s²

Step-by-step explanation:

a) Angular velocity is the ratio of linear velocity and radius.

Here linear velocity = 72 m/s

Radius, r = 0.89 x 0. 5 = 0.445 m

Angular velocity

`\omega =(72)/(0.445)=161.8rad/s`

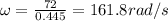
Frequency

`f=(2\pi)/(\omega)=(2* \pi)/(161.8)=0.0388rev/s=2.33rev/min`

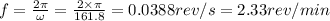
Revolutions per minute = 2.33

b) Centripetal acceleration

`a=(v^2)/(r)`

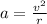
Here linear velocity = 72 m/s

Radius, r = 0.445 m

Substituting

`a=(72^2)/(0.445)=11649.44m/s^2`

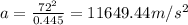
Centripetal acceleration = 11649.44m/s²