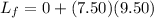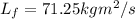Question

A grinding wheel with a mass of 10.50 kg and a radius of 0.55 m is initially at rest. What angular momentum will the wheel have 9.50 s after a 7.50 N·m torque is applied to it.

Answer 1

`L_f = 71.25 kg m^2/s`

Step-by-step explanation:

As we know by Newton's law of rotational motion that Rate of change in angular momentum is total torque on the system

So here we have

`\tau = (\Delta L)/(\Delta t)`

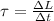
here we can say it

`L_f - L_i = \tau \Delta t`

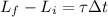
so final angular momentum of the disc is given by the equation

`L_f = L_i + \tau \Delta t`

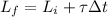
now we know that

`\tau = 7.50 Nm`

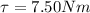
time interval is given as

`\Delta t = 9.50 s`

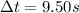
since it is initially at rest so initial angular momentum is ZERO

so we have

`L_f = 0 + (7.50)(9.50)`

`L_f = 71.25 kg m^2/s`