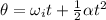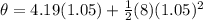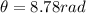Question

Blades of an airplaneâs engine rotate with an initial speed is 40 rev/min. Assuming constant angular acceleration of magnitude 8 rad/s^2 . (a) how long does it take for the blades to reach the angular speed Ïf = 120 rev/ min?

(b)Through how many radians does a blade turn during the time found in (a).
Note : Write down the detail process

Answer 1

Part a)

t = 1.05 s

Part b)

`\theta = 8.78 rad`

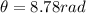
Step-by-step explanation:

Initial angular speed is given as

`\omega_i = 40 rev/min = 0.66 rev/s`

`\omega_i = 2\pi (0.66) = 4.19 rad/s`

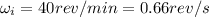
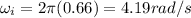
angular acceleration is given as

`\alpha = 8 rad/s^2`

now we have

part a)

final angular speed = 120 rev/min

`\omega_f = 2\pi((120)/(60) rev/s)`

`\omega_f = 12.57 rad/s`

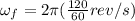
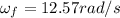
now by kinematics we have

`\omega_f = \omega_i + \alpha t`

`12.57 = 4.19 + 8 t`

`t = 1.05 s`

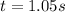
Part b)

Angle turned by the blades is given by

`\theta = \omega_i t + (1)/(2)\alpha t^2`

`\theta = 4.19(1.05) + (1)/(2)(8)(1.05)^2`

`\theta = 8.78 rad`