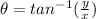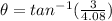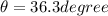Question

Consider a vector 4.08 + 3.0 , wherex, are the unit vectors in x-, y-directions, respectively. (a) What is the magnitude of the vector A? (b) What are the angles vector A makes with the x and y axes, respectively?

Answer 1

Part a)

Magnitude = 5.06 unit

Part b)

`\theta = 36.2 ^0`

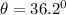
Step-by-step explanation:

Part a)

Vector is given as

`\vec A = 4.08 \hat x + 3.0 \hat y`

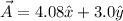
now from above we can say that

x component of the vector is 4.08

y component of the vector is given as 3.0

so the magnitude of the vector is given as

`|A| = √(4.08^2 + 3^2)`

`|A| = 5.06 unit`

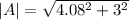
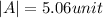
Part b)

Now the angle made by the vector is given as

`\theta = tan^(-1)((y)/(x))`

`\theta = tan^(-1)((3)/(4.08))`

`\theta = 36.3 degree`