For any equation,
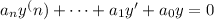
assume solution of a form,
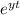
Which leads to,
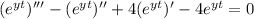
Simplify to,
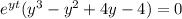
Then find solutions,
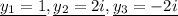
For non repeated real root y, we have a form of,
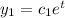
Following up,
For two non repeated complex roots
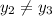 where,
where,
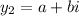
and,
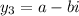
the general solution has a form of,
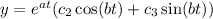
Or in this case,
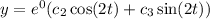
Now we just refine and get,
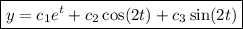
Hope this helps.
r3t40