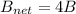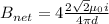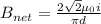Question

A counterclockwise current runs through a square wire loop in the xy plane centered at the origin. The length of each side is d. What is the magnetic field on the z axis?

Answer 1

`B_(net) = (2\sqrt2 \mu_0 i)/(\pi d)`

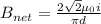
Step-by-step explanation:

Magnetic field due to straight current carrying wire is given by the formula

`B = (\mu_0 i)/(4\pi r)(sin\theta_1 + sin\theta_2)`

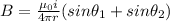
now we will have for one side of the square at its center position given as

`B = (\mu_0 i)/(4\pi ((d)/(2)))(sin45 + sin45)`

`B = (2\sqrt2 \mu_0 i)/(4 \pi d)`

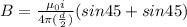
now for the we have for complete square loop it will become 4 times of the one side

`B_(net) = 4 B`

`B_(net) = 4 (2\sqrt2 \mu_0 i)/(4 \pi d)`

`B_(net) = (2\sqrt2 \mu_0 i)/(\pi d)`