Question

Taking the speed of light in vacuum to be 3.000 x 10^8 m/s, find the speed of light in: a. air b. diamond c. crown glass d. water Data: nair =1.0003; ndiamond = 2.420; nwater = 1.340 ncrown glass = 1.500

Answer 1

Step-by-step explanation:

The speed of light in vacuum is, c = 3 × 10⁸ m/s

We have to find the speed of light :

(a) In air :

`n_1_(air)=1.0003`

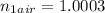
The equation of refractive index is given as :

`n_1=(c)/(v_1)`

`v_1=(c)/(n_1)`

`v_1=(3* 10^8\ m/s)/(1.0003)`

`v_1=299910026.9\ m/s`

`v_1=2.99* 10^8\ m/s`

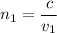
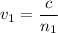
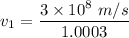
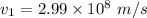
(b) In diamond :

`n_2_(diamond)=2.42`

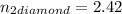
The equation of refractive index is given as :

`n_2=(c)/(v_2)`

`v_2=(c)/(n_2)`

`v_2=(3* 10^8\ m/s)/(2.42)`

`v_2=123966942.1\ m/s`

`v_2=1.23* 10^8\ m/s`

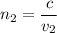
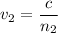
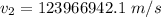
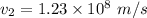
(c) In crown glass :

`n_3_(glass)=1.5`

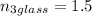
The equation of refractive index is given as :

`n_3=(c)/(v_3)`

`v_3=(c)/(n_3)`

`v_3=(3* 10^8\ m/s)/(1.5)`

`v_3=200000000\ m/s`

`v_3=2* 10^8\ m/s`

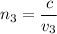
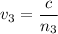
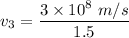
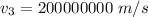
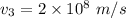
(4) In water :

`n_4_(glass)=1.34`

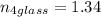
The equation of refractive index is given as :

`n_4=(c)/(v_4)`

`v_4=(c)/(n_4)`

`v_4=(3* 10^8\ m/s)/(1.34)`

`v_4=223880597.01\ m/s`

`v_4=2.23* 10^8\ m/s`

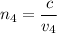
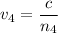
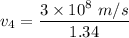
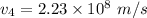
Hence, this is the required solution.