Question

A 1500-kg car traveling at 30 m/s east collides with a 3000-kg car traveling at 20 m/s south. The two cars stick together after the collision. What is the speed of the cars after collision?

Answer 1

Speed of the cars after the collision is 3.34 m/s.

Step-by-step explanation:

It is given that,

Mass of one car, m₁ = 1500 kg

Velocity of this car, v₁ = + 30 m/s ( in east )

Mass of other car, m₂ = 3000 kg

Velocity of other car, v₂ = - 20 m/s (in south)

The two cars stick together after the collision. It is a case of inelastic collision. Let v is the speed of cars after collision. It can be calculated using the conservation of linear momentum as :

`m_1v_1+m_2v_2=(m_1+m_2)v`

`v=(m_1v_1+m_2v_2)/((m_1+m_2))`

`v=(1500\ kg* 30\ m/s+3000\ kg* (-20\ m/s))/(1500\ kg+3000\ kg)`

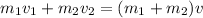
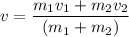
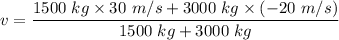
v = -3.34 m/s

So, the speed of the cars after the collision is 3.34 m/s. Hence, this is the required solution.