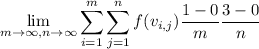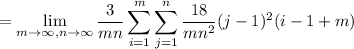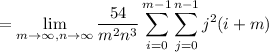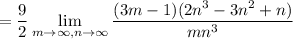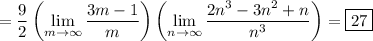Looks like the integral is
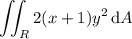
where
![R=[0,1]*[0,3]](https://img.qammunity.org/2020/formulas/mathematics/college/w06rb6lomnfjnzkpt9o57cmimil15eekma.png) . (The inclusion of
. (The inclusion of
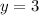 will have no effect on the value of the integral.)
will have no effect on the value of the integral.)
Let's split up
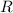 into
into
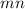 equally-sized rectangular subintervals, and use the bottom-left vertices of each rectangle to approximate the integral. The intervals will be partitioned as
equally-sized rectangular subintervals, and use the bottom-left vertices of each rectangle to approximate the integral. The intervals will be partitioned as
![[0,1]=\left[0,\frac1m\right]\cup\left[\frac1m,\frac2m\right]\cup\cdots\cup\left[\frac{m-1}m,1\right]](https://img.qammunity.org/2020/formulas/mathematics/college/8ctom7yfxuiu4g1tkd35skpfhfakty4tn4.png)
and
![[0,3]=\left[0,\frac3n\right]\cup\left[\frac3n,\frac6n\right]\cup\cdots\cup\left[\frac{3(n-1)}n,3\right]](https://img.qammunity.org/2020/formulas/mathematics/college/lejdldkga97zhslws9l0gw64z22r7s3ymq.png)
where the bottom-left vertices of each rectangle are given by the sequence
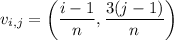
with
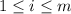 and
and
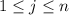 . Then the Riemann sum is
. Then the Riemann sum is