Question

A uniform thin rod is hung vertically from one end and set into small amplitude oscillation. If the rod has a length of 3.6 m, this rod will have the same period as a simple pendulum of length ____ cm. Round your answer to the nearest whole number.

Answer 1

The length of the simple pendulum is 2.4 meters.

Step-by-step explanation:

Time period of simple pendulum is given by :

`T=2\pi\sqrt{(L)/(g)}`

L is the length of pendulum

The time period of the rope is given by :

`T=2\pi\sqrt{(2L')/(3g)}`

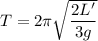
L' is the length of the rod, L' = 3.6 m

It is given that, the rod have the same period as a simple pendulum and we need to find the length of simple pendulum i.e.

`2\pi\sqrt{(L)/(g)}=2\pi\sqrt{(2L')/(3g)}`

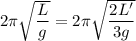
On solving the above equation as :

`(L)/(g)=(2L')/(3g)`

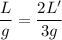
L = 2.4 m

So, the length of the thin rod that is hung vertically from one end and set into small amplitude oscillation 2.4 meters. Hence, this is the required solution.