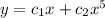Question

the solution of the differential equation x^2y"-5xy'+5y=0 is select the correct answer. (a)y=c1x+c2x^2, (b)y=c1xcoslnx+c2x^2sinlnx, (c)y=c1xcos2lnx+c2x^2sin2lnx, (d) c1x^(5+rad5/2)+c2x^(5-rad5/2) , or (e)y=c1e^2x+c2xe^2xsinx

Answer 1

`y=c_1x+c_2x^5`

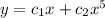
Explanation:

The given second order homogeneous Cauchy-Euler ordinary differential equation is

`x^2y''-5xy'+5y=0`

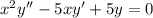
The corresponding auxiliary equation is given by:

`a {m}^(2) + (b - a)m + c = 0`

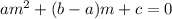
where a=1, b=-5, c=5

We substitute the coefficients into the auxiliary equation to obtain:

`{m}^(2) + ( - 5 - 1)m + 5= 0`

`{m}^(2) - 6m + 5= 0`

`(m - 1)(m - 5) = 0`

`\implies \: m = 1 \: or \: m = 5`

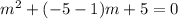
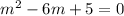
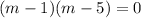
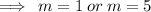
The auxiliary equation has two distinct real roots. The general solution to the corresponding differential equation is of the form:

`y=c_1x ^(m1) +c_2 {x}^(m2)`

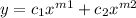
We substitute the values to get:

`y=c_1x+c_2x^5`