Question

A hoop (I = MR2) of mass 3 kg and radius 1.1 m is rolling at a center-of-mass speed of 11 m/s. An external force does 842 J of work on the hoop. What is the new speed of the center of mass of the hoop (in m/s)? Round your answer to the nearest whole number.

Answer 1

`v_f = 20 m/s`

Step-by-step explanation:

Since the hoop is rolling on the floor so its total kinetic energy is given as

`KE = (1)/(2)mv^2 + (1)/(2) I\omega^2`

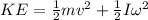
now for pure rolling condition we will have

`v = R\omega`

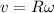
also we have

`I = mR^2`

now we will have

`KE = (1)/(2)mv^2 + (1)/(2)(mR^2)(v^2)/(R^2)`

`KE = mv^2`

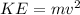
now by work energy theorem we can say

`W = KE_f - KE_i`

`842 J = mv_f^2 - mv_i^2`

`842 = 3(v_f^2) - 3* 11^2`

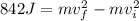
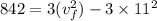
now solve for final speed

`v_f = 20 m/s`