Question

12. True/False and explain your answers. a) If A is invertible then det(A)det(A-1) = 1 b) Any matrix with a row of all zeros has a determinant of 1. c) If A is a skew symmetric matrix, AT = -A, and A has size n x n then A must be singular if n is odd.

Answer 1

Answer with explanation:

(A)

It is given that, A is invertible, That is inverse of matrix exist.

`|A|=|A^(-1)|\\eq 0`

That is,
`|A|=|A^(-1)|=1`, is incorrect Statement.

False

(B)

If a Matrix has , either any row or column has all entry equal to Zero, then value of Determinant is equal to 0.

Any matrix with a row of all zeros has a determinant of 1 ,is incorrect Statement.

False

(C)

The Meaning of Singular matrix is that , then Determinant of Singular Matrix is equal to Zero.

For, a n×n , matrix, whether n is Odd or even

`A^(T)= -A\\\\|A^(T)|=|-A|=(-1)^n|A|`

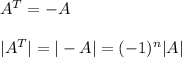
So, the statement, If A is a skew symmetric matrix,
`A^(T)= -A`,and A has size n x n then A must be singular if n is odd ,is incorrect Statement.

False