Question

An object at the surface of Earth (at a distance R from the center of Earth) weighs 166 N. What is its weight (in N) at a distance 4R from the center of Earth? Round your answer to the nearest tenth.

Answer 1

The weight at a distance 4R from the center of earth is 10.37 N.

Step-by-step explanation:

Given that,

Weight = 166 N

Distance = 4R

Let m be the mass of the object.

We know that,

Mass of earth
`M_(e)=5.98*10^(24)\ kg`

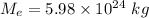
Gravitational constant
`G = 6.67*10^(-11)\ N-m^2/kg^2`

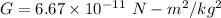
Radius of earth
`R = 6.38*10^(6)\ m`

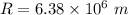
We need to calculate the weight at a distance 4 R from the center of earth

Using formula of gravitational force

`W = (GmM_(e))/(R^2)`

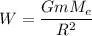
Put the value in to the formula

`166=(6.67*10^(-11)* m*5.98*10^(24))/((6.38*10^(6))^2)`

`m=(166*(6.38*10^(6))^2)/(6.67*10^(-11)*5.98*10^(24))`

`m=16.94 kg`

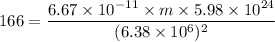
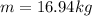
Now, Again using formula of gravitational

`W=(6.67*10^(-11)* 16.94*5.98*10^(24))/((4*6.38*10^(6))^2)`

`W=10.37 N`

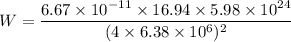
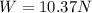
Hence, The weight at a distance 4R from the center of earth is 10.37 N.