Question

On takeoff, the combined action of the engines and the wings of an airplane exert a force of 8.00 × 103 N on the plane upward at an angle of 65.0" above the horizontal. The plane rises with constant velocity in the vertical direction while continuing to accelerate in the horizontal direction. (3 marks) a. What is the weight of the plane? b. What is the horizontal acceleration of the plane? .

Answer 1

a) 7250.5 N

b) 4.6 m/s²

Step-by-step explanation:

a)

F = applied force = 8000 N

θ = angle with the horizontal = 65 deg

Consider the motion along the vertical direction :

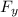`F_(y)` = Applied force in vertical direction in upward direction = F Sinθ = 8000 Sin65 = 7250.5 N

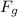`F_(g)` = weight of the plane in vertical direction in downward direction = ?

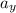`a_(y)` = Acceleration in vertical direction = 0 m/s²

Taking the force in upward direction as positive and in downward direction as negative, the force equation along the vertical direction can be written as

`F_(y)-F_(g) = m a_(y)`

`7250.5 -F_(g) = m (0)`

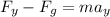
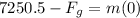
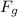`F_(g)` = 7250.5 N

b)

m = mass of the plane

force of gravity is given as

`F_(g) = mg`

`7250.5 = m(9.8)`

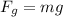
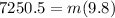
m = 739.85 kg

Consider the motion along the horizontal direction

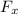`F_(x)` = Applied force in horizontal direction = F Cosθ = 8000 Cos65 = 3381 N

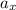`a_(x)` = Acceleration in horizontal direction

Acceleration in horizontal direction is given as

`a_(x)=(F_(x))/(m)`

`a_(x)=(3381)/(739.85)`

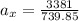
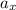`a_(x)` = 4.6 m/s²