Answer:
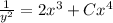 .
.
Explanation:
Given differential equation
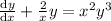
Differential equation can be write as
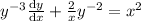
By Bernoulli method
Susbstitute
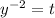 .....{equationI}
.....{equationI}
Differentiate equation I w.r.t x then we get
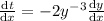
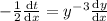
Susbstitute the values in the given differential equation then we get
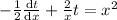
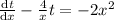
It is first order linear differential equation and compare with the first order linear differential equation
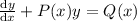
Then we get P(x)=
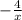 and Q(x)=
and Q(x)=
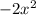
Integration factor=
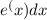
Integration factor=
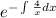
Integration factor=
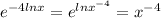 .
.
Using
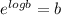
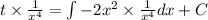
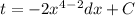
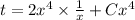
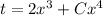
Substitute
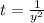 then we get
then we get
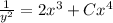 .
.
Answer:
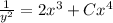 .
.