Question

Determine the energy required to accelerate an electron between each of the following speeds. (a) 0.500c to 0.900c MeV (b) 0.900c to 0.942c MeV

Answer 1

The energy required to accelerate an electron is 0.582 Mev and 0.350 Mev.

Step-by-step explanation:

We know that,

Mass of electron
`m_(e)=9.11*10^(-31)\ kg`

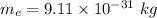
Rest mass energy for electron = 0.511 Mev

(a). The energy required to accelerate an electron from 0.500c to 0.900c Mev

Using formula of rest,

`E=\frac{E_(0)}{\sqrt{1-(v_(f)^2)/(c^2)}}-\frac{E_(0)}{\sqrt{1-(v_(i)^2)/(c^2)}}`

`E=\frac{0.511}{\sqrt{1-((0.900c)^2)/(c^2)}}-\frac{0.511}{\sqrt{1-((0.500c)^2)/(c^2)}}`

`E=0.582\ Mev`

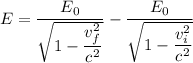
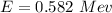
(b). The energy required to accelerate an electron from 0.900c to 0.942c Mev

Using formula of rest,

`E=\frac{E_(0)}{\sqrt{1-(v_(f)^2)/(c^2)}}-\frac{E_(0)}{\sqrt{1-(v_(i)^2)/(c^2)}}`

`E=\frac{0.511}{\sqrt{1-((0.942c)^2)/(c^2)}}-\frac{0.511}{\sqrt{1-((0.900c)^2)/(c^2)}}`

`E=0.350\ Mev`

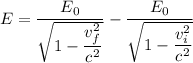
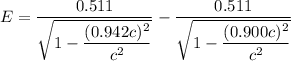
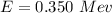
Hence, The energy required to accelerate an electron is 0.582 Mev and 0.350 Mev.