Question

Determine the capacitive reactance for a 20 uF capacitor that is across a 20 volt, 60 Hz source

Answer 1

Capacitive reactance is 132.6 Ω.

Step-by-step explanation:

It is given that,

Capacitance,
`C=20\ \mu F=20* 10^(-6)\ F=2* 10^(-5)\ F`

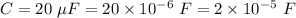
Voltage source, V = 20 volt

Frequency of source, f = 60 Hz

We need to find the capacitive reactance. It is defined as the reactance for a capacitor. It is given by :

`X_C=(1)/(2\pi fC)`

`X_C=(1)/(2\pi * 60\ Hz* 2* 10^(-5)\ F)`

`X_C=132.6\ \Omega`

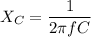
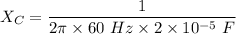
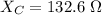
So, the capacitive reactance of the capacitor is 132.6 Ω. Hence, this is the required solution.