Question

How large must the coefficient of static friction be between the tires and the road if a car is to round a level curve of radius 120 m at a speed of 119 km/h 7 Express your answer using two significant figures

Answer 1

Coefficient of static friction between the tires and the road is 0.92.

Step-by-step explanation:

It is given that,

Radius of the curve, r = 120 m

Speed, v = 119 km/h = 33.05 m/s

We need to find the coefficient of static friction between the tires and the road. In a curved road the safe velocity is given by :

`v=√(\mu rg)`

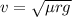
`\mu` is the coefficient of static friction

g is acceleration due to gravity

`\mu=(v^2)/(rg)`

`\mu=((33.05\ m/s)^2)/(120\ m* 9.8\ m/s^2)`

`\mu=0.92`

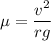
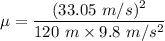
So, the coefficient of static friction between the tires and the road is 0.92. Hence, this is the required solution.