Question

Alexa pays 7/20 of a dollar for each minute she uses her pay-as-you-go phone for a call, and 2/5 of a dollar for each minute of data she uses. This month, she used a total of 85 minutes and the bill was $31. Which statements are true? Check all that apply.

The system of equations is x + y = 31 and 7/20x+2/5y=85
The system of equations is x + y = 85 and 7/20x+2/5y=31
To eliminate the y-variable from the equations, you can multiply the equation with the fractions by 5 and leave the other equation as it is.
To eliminate the x-variable from the equations, you can multiply the equation with the fractions by 20 and multiply the other equation by -7.
A-She used 25 minutes for calling and 60 minutes for data.
B-She used 60 minutes for calling and 25 minutes for data.
C-She used 20 minutes for calling and 11 minutes for data.
D-She used 11 minutes for calling and 20 minutes for data.

Answer 1

The second, fourth and B option are correct.

Explanation:

In order to solve this problem, we are going to define the following variables :

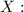`X:` ''Minutes she used her pay-as-you-go phone for a call''

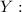`Y:` ''Minutes of data she used''

Then, we are going to make a linear system of equations to find the values of
`X` and
`Y`.

''This month, she used a total of 85 minutes'' ⇒

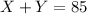`X+Y=85` (I)

(I) is the first equation of the system.

''The bill was $31'' ⇒

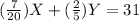`((7)/(20))X+((2)/(5))Y=31` (II)

(II) is the second equation of the system.

The system of equations will be :

`\left \{ {{X+Y=85} \atop {((7)/(20))X+((2)/(5))Y=31}} \right.`

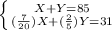
The second option ''The system of equations is
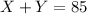`X+Y=85` and
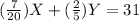`((7)/(20))X+((2)/(5))Y=31` .'' is correct

Now, to solve the system, we can eliminate the x-variable from the equations by multiplying the equation with the fractions by 20 and multiplying the other equation by -7. Then, we can sum them to obtain the value of
`Y` :

`X+Y=85` (I)

`((7)/(20))X+((2)/(5))Y=31` (II) ⇒

`(-7)X+(-7)Y=-595` (I)'

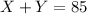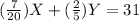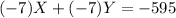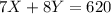`7X+8Y=620` (II)'

If we sum (I)' and (II)' ⇒

`(-7)X+(-7)Y+7X+8Y=-595+620` ⇒
`Y=25`

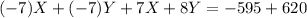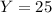
If we replace this value of
`Y` in (I) ⇒

`X+Y=85\\X+25=85\\X=60`

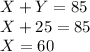
The fourth option ''To eliminate the x-varible from the equations, you can multiply the equation with the fractions by 20 and multiply the other equation by -7'' is correct.

With the solution of the system :

`\left \{ {{X=60} \atop {Y=25}} \right.`

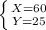
We answer that the option ''B-She used 60 minutes for calling and 25 minutes for data'' is correct.

Answer 2

• The system of equations is x + y = 85 and 7/20x+2/5y=31
• To eliminate the x-variable from the equations, you can multiply the equation with the fractions by 20 and multiply the other equation by -7.
• B-She used 60 minutes for calling and 25 minutes for data.

Explanation:

It is always a good idea to start by defining variables in such a problem. Here, we can let x represent the number of calling minutes, and y represent the number of data minutes. The the total number of minutes used is ...

x + y = 85

The total of charges is the sum of the products of charge per minute and minutes used:

7/20x + 2/5y = 31.00

We can eliminate the x-variable in these equations by multiplying the first by -7 and the second by 20, then adding the result.

-7(x +y) +20(7/20x +2/5y) = -7(85) +20(31)

-7x -7y +7x +8y = -595 +620 . . . . eliminate parentheses

y = 25 . . . . . . . . simplify

Then the value of x is

x = 85 -y = 85 -25

x = 60