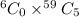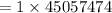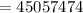Question

From a shipment of 65 transistors, 6 of which are defective, a sample of 5 transistors is selected at random.

(a) In how many different ways can the sample be selected?
________ways

(b) How many samples contain exactly 3 defective transistors?
________samples

(c) How many samples do not contain any defective transistors?
________ samples

Answer 1

a) 8259888

b) 34220

c) 45057474

Explanation:

Given,

The total number of transistor = 65,

In which, the defective transistor = 6,

So, the number of non defective transistor = 65 - 6 = 59,

Since, out of these transistor 5 are selected,

a) Thus, the number of ways = the total possible combination of 5 transistors =
`{65}C_ 5`

`=(65!)/((65-5)!5!)`

`=8259888`

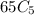
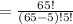
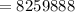
b) The number of samples that contains exactly 3 defective transistors = the possible combination of exactly 3 defective transistors =
`{6}C_3* {59}C_2`

`=(6!)/((6-3)!3!)* (59!)/((59-2)!* 2!)`

`=20* 1711`

`=34220`

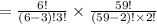
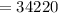
c) The number of sample without any defective transistor = The possible combination of 0 defective transistor =
`^6C_0* ^(59)C_5`

`=1* 45057474`

`=45057474`