Question

PROBLEM 1 Verify that the differential equation (2x y)dx +(x - 6y)dy = 0 is exact and then solve the associated differential equation

Answer 1

Answer with explanation:

⇒(2 x y )d x+(x-6 y) d y=0

P= 2 x y

Q=x-6 y

`P_(y)=2 x\\\\Q_(x)=1`

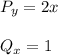
So this Differential Equation is exact.

To solve this, we will first evaluate,
`\varphi (x,y)`.

`\varphi_(x)=P\\\\\varphi_(y)=Q\\\\\varphi=\int P d x\\\\= \int 2 x y  dx\\\\\varphi=x^2 y\\\\\varphi(x,y)=x^2y+k(y)------(1)`

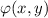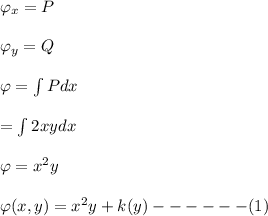
Differentiating with respect to , y

`\varphi'(x,y)=x^2+k'(y)=Q=x-6 y\\\\\rightarrow x-6 y-x^2=k'(y)\\\\ k(y)=\int (x-6 y -x^2) dy\\\\k(y)=x y-3 y^2-x^2 y+f\\\\\varphi(x,y)=x^2y+x y-3 y^2-x^2 y+f\\\\\varphi(x,y)=x y-3 y^2+f`

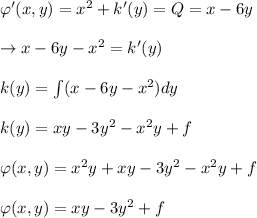
Substituting the value of , k(y) in equation 1.

This is required Solution of exact differential equation.