Question

Solve y''+2y' - 3y = 0, y(0) = 3, y'(0) = 11 Preview y(t) = |2e^(-3t)+5e^t Points possible: 1 This is attempt 3 of 3 Score on last attempt: 0. Score in gradebook: 0 License Submit

Answer 1

`y''+2y'-3y=0`

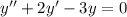
Second order linear homogeneous differential equation with constant coefficients, ODE has a form of,

`ay''+by'+cy=0`

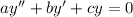
From here we assume that for any equation of that form has a solution of the form,
`e^(yt)`

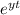
Now the equation looks like this,

`((e^(yt)))''+2((e^(yt)))'-3e^(yt)=0`

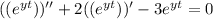
Now simplify to,

`e^(yt)(y^2+2y-3)=0`

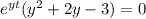
You can solve the simplified equation using quadratic equation since,

`e^(yt)(y^2+2y-3)=0\Longleftrightarrow y^2+2y-3=0`

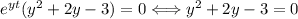
Using the QE we result with,

`\underline{y_1=1}, \underline{y_2=-3}`

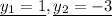
So,

For two real roots
`y_1\\eq y_2` the general solution takes the form of,

`y=c_1e^(y_1t)+c_2e^(y_2t)`

Or simply,

`\boxed{y=c_1e^t+c_2e^(-3t)}`

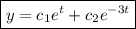
Hope this helps.

r3t40