Question

Write an expression for the area of a square with side s = 2x + 5

Answer 1

`A = 4x ^ 2 + 20x +25`

Explanation:

Remember that all sides of a square have the same length. Therefore, the Area of a square is defined as:

`A = s ^ 2`

Where s is the length of the sides of the squares.

In this case we know that the length of the sides is:

`s = 2x + 5`

So the area is:

`A = (2x +5) ^ 2`

We develop the expression and we have left that the area is:

`A = 4x ^ 2 + 20x +25`

Answer 2

`4x^2+20x+25` square units

Explanation:

We are given that side of a square has the dimension
`s = 2x + 5` and using this, we are to write an expression for the area of this square.

We know that the formula of area of a square is given by:

Area of square =
`s^2`

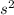
So substituting the given value in the above formula to get:

Area of square =
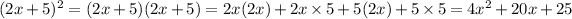`(2x+5)^2 = (2x+5)(2x+5) = 2x(2x)+2x*5+5(2x)+5*5 = 4x^2+20x+25` square units