Question

For the following functions from R -> R, determine if function is one to one, onto, or both. Explain.

a) f(x)=3x-4

b)g(x)=(x^2)-2

c) h(x)=2/x

d) k(x)=ln(x)

e) l(x) = e^x

Answer 1

Answer with explanation:

a. f(x)=3x-4

Let
`f(x_1)=f(x_2)`

`3x_1-4=3x_2-4`

`3x_1=3x_2-4+4`

`3x_1=3x_2`

`x_1=x_2`

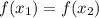
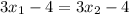
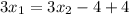
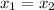
Hence, the function one-one.

Let f(x)=y

`y=3x-4`

`3x=y+4`

`x=(y+4)/(3)`

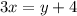
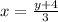
We can find pre image in domain R for every y in range R.

Hence, the function onto.

b.g(x)=
`x^2-2`

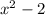
Substiute x=1

Then
`g(x)=1-2=-1`

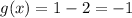
Substitute x=-1

Then g(x)=1-2=-1

Hence, the image of 1 and -1 are same . Therefore, the given function g(x) is not one-one.

The given function g(x) is not onto because there is no pre image of -2, -3,-4...... R.

Hence, the function neither one-one nor onto on given R.

c.
`h(x)=(2)/(x)`

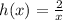
The function is not defined for x=0 .Therefore , it is not a function on domain R.

Let
`h(x_1)=h(x_2)`

`(2)/(x_1)=(2)/(x_2)`

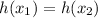
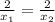
By cross mulitiply

`x_1= (2* x_2)/(2)`

`x_1=x_2`

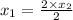
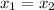
Hence, h(x) is a one-one function on R-{0}.

We can find pre image for every value of y except zero .Hence, the function

h(x) is onto on R-{0}.

Therefore, the given function h(x) is both one- one and onto on R-{0} but not on R.

d.k(x)= ln(x)

We know that logarithmic function not defined for negative values of x. Therefore, logarithmic is not a function R.Hence, the given function K(x) is not a function on R.But it is define for positive R.

Let
`k(x_1)=k(x_2)`

`ln(x_1)=ln(x_2)`

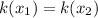
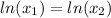
Cancel both side log then

`x_1=x_2`

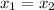
Hence, the given function one- one on positive R.

We can find pre image in positive R for every value of
`y\in R^+`.

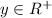Therefore, the function k(x) is one-one and onto on
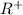`R^+` but not on R.

e.l(x)=
`e^x`

Using horizontal line test if we draw a line y=-1 then it does not cut the graph at any point .If the horizontal line cut the graph atmost one point the function is one-one.Hence, the horizontal line does not cut the graph at any point .Therefore, the function is one-one on R.

If a horizontal line cut the graph atleast one point then the function is onto on a given domain and codomain.

If we draw a horizontal line y=-1 then it does not cut the graph at any point .Therefore, the given function is not onto on R.