Question

Solve for x: x5 + x4 − 7x3 − 7x2 − 144x − 144 = 0

Answer 1

{ -1, -3i,3i,4,-4}

Explanation:

I'm going to try to get the Rational Root Theorem to work for us.

Since the coefficient of leading term is 1 we just need to look at the factors of the constant.

Possible rational zeros are going to be the factors of -144.

So here are some possible rational zeros: 1,2,3,4,6,8,9,12,16,18,24,36,48,72 and also the negative version of these numbers are numbers we must consider.

I'm going to see if -1 works.

(-1)^5+(-1)^4-7(-1)^3-7(-1)^2-144(-1)-144

-1 + 1 +7 -7 +144 -144=0

So -1 is a zero so x+1 is a factor. I'm going to use synthetic division to see what multiplies to x+1 that will me the initial polynomial expression we had.

-1 | 1 1 -7 -7 -144 -144

| -1 0 7 0 144

| ________ __________________

1 0 -7 0 -144 0

So the (x+1)(x^4-7x^2-144)=0

The cool thing is that other factor is a sort of quadratic in disguise. That is it becomes a quadratic if you let u=x^2. So let's do that.

u^2-7u-144=0

(u+9)(u-16)=0

u=-9 or u=16

So x^2=-9 or x^2=16.

Square rooting both sides gives us:

`x= \pm 3i \text{ or } x=\pm 4`

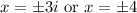
So the solution set is { -1, -3i,3i,4,-4}

Answer 2

`x^5 + x^4 - 7x^3 - 7x^2 -144x - 144 = 0 \\x^4(x+1)-7x^2(x+1)-144(x+1)=0\\(x^4-7x^2-144)(x+1)=0\\\\x+1=0\Rightarrow x=-1\\\\x^4-7x^2-144=0\\x^4-16x^2+9x^2-144=0\\x^2(x^2-16)+9(x^2-16)=0\\(x^2+9)(x^2-16)=0\\(x^2+9)(x-4)(x+4)=0\\\\x^2+9=0\vee x-4=0 \vee x+4=0\\x=4 \vee x=-4\\\\x\in\{-4,-1,4\}`