Step-by-step explanation:
Given that,
Height of object = 4.31 cm
Distance of the object = -12.6 cm
Distance of the image = -8.77 cm
For concave mirror,
Using mirror's formula
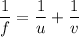
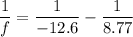

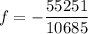

Radius of the mirror is
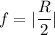
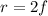
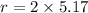
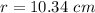
The magnification of the mirror,
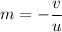
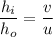
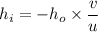

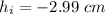
Now, For convex mirror,
Using mirror's formula
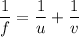
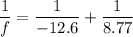
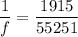
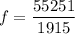
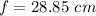
Radius of the mirror is

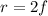

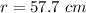
The magnification of the mirror,
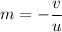
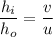
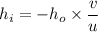
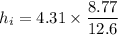
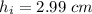
Hence, This is the required solution.