Question

Tickets for a play cost 2 pounds for a child, and 4 pounds for an adult. one adult brought 4 children with him and the remaining adults each brought 2 children with them. The total ticket sales were 60 pounds. how many adults and children were present in that play?

Solve using augmented matrix.

Answer 1

Number of adults = 7

Number of children = 16

Explanation:

Tickets for a play cost 2 pounds for a child, and 4 pounds for an adult.

Let x number of adults and y number of children.

1 child ticket cost = 2 pound

y children ticket cost = 2y pound

1 adult ticket cost = 4 pound

x adults ticket cost = 4x pound

Total number of ticket sales were 60 pounds

Therefore, 4x + 2y = 60 ------------- (1)

One adult brought 4 children with him and the remaining adults each brought 2 children with them.

Remaining number of adult whose brought 2 children = x-1

Number children = 2(x-1)

Total number of children = 2(x-1)+4

Therefore, y=2x+2 ---------------------(2)

System of equation,

2x + y = 30

-2x + y = 2

Using augmented matrix to solve system of equation.

`\begin{bmatrix}2&1&\ |30\\-2&1&|2\end{bmatrix}\\\\R_2\rightarrow R_2+R_1\\\\\begin{bmatrix}2&1& |30\\0&2&|32\end{bmatrix}\\\\R_2\rightarrow(1)/(2)R_2\\`

`\begin{bmatrix}2&1&\ |30\\0&1&|16\end{bmatrix}\\\\R_1\rightarrow R_1-R_2\\\\\begin{bmatrix}2&0&\ |14\\0&1&|16\end{bmatrix}\\\\\\`

`R_1\rightarrow (1)/(2)R_1\\\\\begin{bmatrix}1&0&|7\\0&1&|16\end{bmatrix}\\\\`

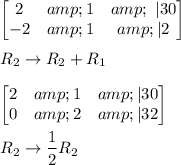
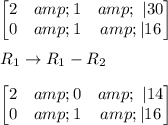
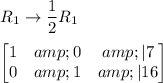
Now, we find the value of variable.

`x=7\text{ and }y=16`

Hence, Number of adults are 7 and Number of children are 16.