Answer:
Part 1)
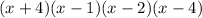
The related polynomial equation has a total of four roots, all four roots are real
Part 2)
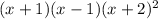
The related polynomial equation has a total of four roots, all four roots are real and one root has a multiplicity of 2
Part 3)
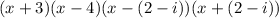
The related polynomial equation has a total of four roots, two roots are complex and two roots are real
Part 4)
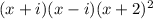
The related polynomial equation has a total of four roots, two roots are complex and one root is real with a a multiplicity of 2
Explanation:
we know that
The Fundamental Theorem of Algebra states that: Any polynomial of degree n has n roots
so
Part 1) we have
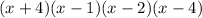
The roots of this polynomial are
x=-4, x=1,x=2,x=4
therefore
The related polynomial equation has a total of four roots, all four roots are real
Part 2) we have
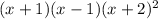
The roots of this polynomial are
x=-1, x=1,x=-2,x=-2
therefore
The related polynomial equation has a total of four roots, all four roots are real and one root has a multiplicity of 2
Part 3) we have
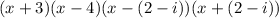
The roots of this polynomial are
x=-3, x=4,x=(2-i),x=-(2-i)
therefore
The related polynomial equation has a total of four roots, two roots are complex and two roots are real
Part 4) we have
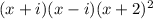
The roots of this polynomial are
x=-i, x=i,x=-2,x=-2
therefore
The related polynomial equation has a total of four roots, two roots are complex and one root is real with a a multiplicity of 2