Question

How to find equation of line passing through the points (x,y)​

Answer 1

First you must acknowledge that you are dealing with a line therefore you must write linear equation or linear function in this case.

Linear function has a form of,

`y=mx+n`

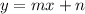
Then calculate the slope m using the coordinates of two points. Let say A(x1, y1) and B(x2, y2),

`m=\frac{\Delta{y}}{\Delta{x}}=(y_2-y_1)/(x_2-x_1)`

Now pick a point either A or B and insert coordinates of either one of them in the linear equation also insert the slope you just calculated, I will pick point A.

`y_1=mx_1+n`

From here you solve the equation for n,

`</p><p>y_1=mx_1+n\Longrightarrow n=y_1-mx_1</p><p>`

So you have slope m and variable n therefore you can write down the equation of the line,

`f(x)=m_(slope)x+n_(variable)`

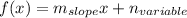
Hope this helps.

r3t40