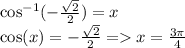Answer:
Explanation:
First, we know that the sin function is odd which means:
sin(-x) = -sin(x).
Secondly evaluating an inverse trigonometric function with a normal trigonometric function as the argument can be rewritten as an algebraic expression.
Let
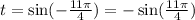
We know the certain identity.
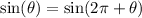
We use it to evaluate sin(11 pi / 4).
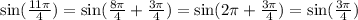
Another helping identity is the following:
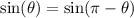
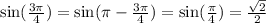
But let's not forget that t = -sin(11 pi/4) = - sqrt(2) / 2
Now we end up with the following equation.